Virtual Lab Tension Test
ELASTIC DEFORMATION IN MATERIALS
The Elastic Response
Close the window to return to the tension test
We will first discuss the elastic response of a metal. As seen from the Figure 1, the elastic stress-strain response is a straight line, or in other words, the response is linear. If the material is unloaded in the elastic region it returns to its original unloaded state along this straight line. Linear elastic behavior is intrinsically related to the nature of atomic bonding and is discussed later in this section.
When a uni-axial tensile stress is applied to the specimen, it extends along the tensile axis and undergoes transverse contraction along the two perpendicular axes (see Figure 2).
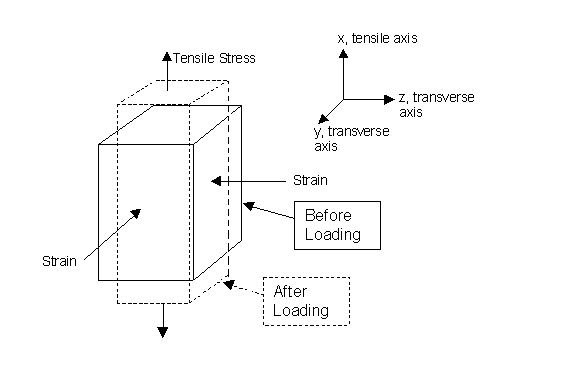
Figure 2. Elastic tensile deformation of a specimen
For linear elastic deformation, the longitudinal and transverse strains are related through the equation
![]()
where n is called the Poisson’s ratio and is a property of the material. The negative sign indicates that the dimensions of the specimen along the transverse axes decrease as the length of the specimen along the tensile axis increases. The slope of the straight line in the linear elastic region is called the Young’s modulus or the elastic modulus, E, of the material. E is also a property of the material. Following elastic deformation, plastic (or permanent) flow commences at a stress equal to the yield strength, Sy. If the material is loaded to or beyond the yield strength and then unloaded, it does not return to its original unloaded state, but retains some deformation, which is explained further in the discussion on plastic region.
It may be pointed out that the volume of a material increases slightly during elastic tensile deformation and decreases during elastic compression. During plastic deformation the volume of the material is conserved. In the elastic region, a linear relationship exists between stress and strain, called Hooke’s Law. For a 3- dimensional deformation, the tensile stress – strain laws are:
![]()
![]()
![]() (2)
(2)
![]()
If pure shear stresses are applied, the elastic response of the material is characterized by the shear modulus, G, and the six shear stresses are related to the six shear strains by the relations
![]()
![]()
![]() (3)
(3)
![]()
![]()
![]()
Hence, for an isotropic material only two of the material properties G, E, and n, are independent, while the third can be calculated from the relation
![]() (4)
(4)